"Символ Логики" инструкция
1. Условия эксплуатации
Не пишите на Кольцах
Не деформируйте Кольца
Не разбирайте Куб
Для чистки используйте сухую мягкую ткань
Для надписей на Кубе используйте стираемый маркер на водной основе
Храните маркер с плотно надетым колпачком
Не деформируйте Кольца
Не разбирайте Куб
Для чистки используйте сухую мягкую ткань
Для надписей на Кубе используйте стираемый маркер на водной основе
Храните маркер с плотно надетым колпачком
2. Комплектация
• Куб Понятий — 1 шт.
• Кольца Умозаключений — 5 шт.
• Инструкция — 1 шт.
• Коробка — 1 шт.
• Кольца Умозаключений — 5 шт.
• Инструкция — 1 шт.
• Коробка — 1 шт.
3. Введение
Наверняка Вы слышали о психологическом приеме для создания правильного настроя и придания жизненных сил, который называется аффирмацией. И конечно интуитивно пользовались им, даже не имея глубоких познаний в психологии. Аффирмации это различные позитивные утверждения, регулярное повторение которых является эффективным средством самовнушения и используется в аутотренинге.
Набор «Символ Логики» служит инструментом, усиливающим положительное воздействие аффирмаций путем создания и наглядной визуализации их логически безупречных композиций. Он позволяет:
• формулировать аффирмации в соответствии с правилами логики;
• автоматически строить на основе аффирмации различные высказывания, выражающие ту же мысль;
• связывать мысли в логически непротиворечивое умозаключение;
• представлять сочетание аффирмаций в виде пространственной композиции.
Набор «Символ Логики» служит инструментом, усиливающим положительное воздействие аффирмаций путем создания и наглядной визуализации их логически безупречных композиций. Он позволяет:
• формулировать аффирмации в соответствии с правилами логики;
• автоматически строить на основе аффирмации различные высказывания, выражающие ту же мысль;
• связывать мысли в логически непротиворечивое умозаключение;
• представлять сочетание аффирмаций в виде пространственной композиции.
4. Аффирмации как логические суждения
Аффирмации выражают некоторые суждения, и с точки зрения логики их можно подразделить на общие и частные. Аффирмации в форме общего суждения максимально жизнеутверждающие, например такие как «Все у меня замечательно» или «Все мои мечты исполнятся». Но иногда бывают полезны менее сильные аффирмации в форме частных суждений, которые относятся не ко всем, а лишь к некоторым вещам, например, «Некоторые черты моего характера уникальные» или «Некоторые обиды можно простить».
Используя «Символ Логики», стройте аффирмации в соответствии с правилами логики: сильные общие аффирмации с помощью кванторного слова «все», а более слабые частные — с помощью кванторного слова «некоторые».
Аффирмации могут быть утвердительными или отрицательными. Отрицательные содержат знак отрицания «не», как, например, аффирмация «Все проблемы не страшны».
Используя «Символ Логики», стройте аффирмации в соответствии с правилами логики: сильные общие аффирмации с помощью кванторного слова «все», а более слабые частные — с помощью кванторного слова «некоторые».
Аффирмации могут быть утвердительными или отрицательными. Отрицательные содержат знак отрицания «не», как, например, аффирмация «Все проблемы не страшны».
5. Аффирмация как отношение двух понятий
Каждая аффирмация говорит о неком конкретном предмете, к примеру: мои мысли; способности; перемены; проблемы; мечты; желания; моё тело; известия; неприятности; дни моей жизни; клетки организма; близкие; сплетни; будущее; здоровье; коллеги; болезни; цели; задачи; чувства; события; потери; усилия; отношения; деньги; недоброжелатели.
В отношении любого из этих (и прочих) предметов аффирмация дает установку в виде определенного качества или действия. Например: радостные; в моих руках; сбудутся/не сбудутся; прекрасные; наполняют меня; значимые/не значимые; достойные; к лучшему; принимаю/не принимаю; любимые; к достатку; будут успешны/не будут успешны; уверенные; ведут к победе; сильные/не сильные; здоровые; делают сильнее; большие/не большие.
В отношении любого из этих (и прочих) предметов аффирмация дает установку в виде определенного качества или действия. Например: радостные; в моих руках; сбудутся/не сбудутся; прекрасные; наполняют меня; значимые/не значимые; достойные; к лучшему; принимаю/не принимаю; любимые; к достатку; будут успешны/не будут успешны; уверенные; ведут к победе; сильные/не сильные; здоровые; делают сильнее; большие/не большие.
6. Композиция аффирмаций
Аффирмации получают большую убедительную силу, когда образуют логически связанную композицию. Для этого две аффирмации должны содержать одинаковое понятие, тогда их можно связать в умозаключение.
Например, аффирмации «Все органы моего тела здоровые» и «Все здоровые хорошо работают» содержат понятие «здоровые». Благодаря чему из них следует логически верное заключение «Все органы моего тела хорошо работают», усиливающее исходную аффирмацию.
Или если взять аффирмации «Все мои мысли — конструктивные» и «Некоторые мои фантазии — конструктивные», то вторая из них логически связывается с первой суждением «Некоторые мои мысли — фантазии».
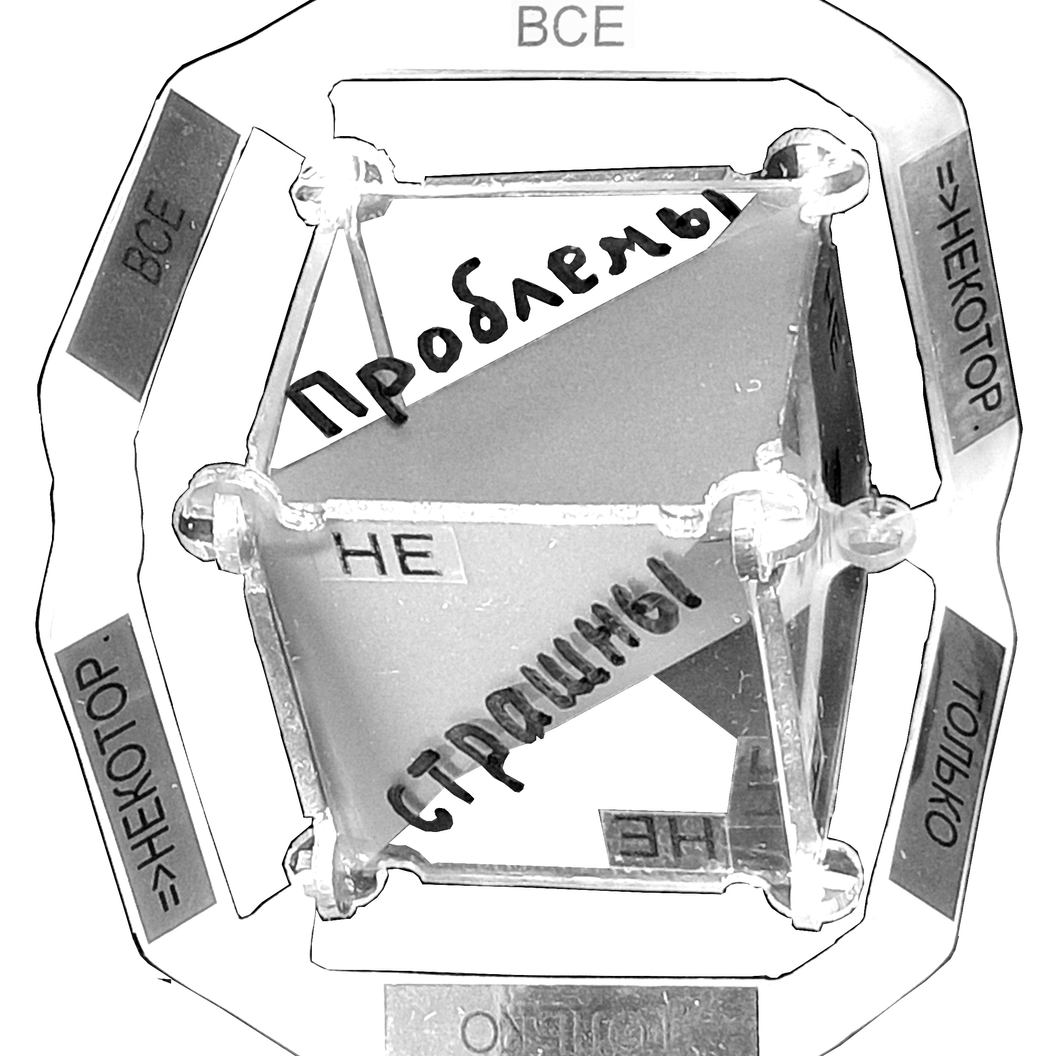
Такие композиции аффирмаций создаются с помощью набора «Символ Логики» путем записи входящих в аффирмации понятий на грани Куба Понятий с последующим прикреплением к нему одного из Колец Умозаключений. Имеющиеся на Кольце кванторные слова вместе с записанными на Кубе понятиями и знаками отрицания образуют силлогистическое умозаключение, усиливающее аффирмации.
Например, аффирмации «Все органы моего тела здоровые» и «Все здоровые хорошо работают» содержат понятие «здоровые». Благодаря чему из них следует логически верное заключение «Все органы моего тела хорошо работают», усиливающее исходную аффирмацию.
Или если взять аффирмации «Все мои мысли — конструктивные» и «Некоторые мои фантазии — конструктивные», то вторая из них логически связывается с первой суждением «Некоторые мои мысли — фантазии».
Такие композиции аффирмаций создаются с помощью набора «Символ Логики» путем записи входящих в аффирмации понятий на грани Куба Понятий с последующим прикреплением к нему одного из Колец Умозаключений. Имеющиеся на Кольце кванторные слова вместе с записанными на Кубе понятиями и знаками отрицания образуют силлогистическое умозаключение, усиливающее аффирмации.
7. Использование Куба Понятий
Построение аффирмации или суждения начните с определения того, какие два понятия связывает эта аффирмация или суждение. Каждое из выявленных понятий запишите на одной из граней Куба Понятий, используя стираемый маркер на водной основе. Это же понятие надо записать повторно на противоположной грани Куба, так чтобы оно было записано на грани со знаком отрицания «НЕ» и на грани без этого знака.
Понятия предпочтительно записывать в грамматической форме имен существительных, прилагательных или причастий во множественном числе, это облегчит последующее прочтение получившихся высказываний. При необходимости используйте сокращения.
Надписи удобнее делать по диагонали. Для их правки используйте стирающую губку на колпачке маркера. Не допускайте касания маркером Колец Умозаключений, так как следы маркера с них трудно стираются.
Для построения одной аффирмации или суждения достаточно записи на Кубе двух понятий. Для добавления второй аффирмации и построения умозаключения запишите на Кубе третье понятие и продублируйте его.
Понятия предпочтительно записывать в грамматической форме имен существительных, прилагательных или причастий во множественном числе, это облегчит последующее прочтение получившихся высказываний. При необходимости используйте сокращения.
Надписи удобнее делать по диагонали. Для их правки используйте стирающую губку на колпачке маркера. Не допускайте касания маркером Колец Умозаключений, так как следы маркера с них трудно стираются.
Для построения одной аффирмации или суждения достаточно записи на Кубе двух понятий. Для добавления второй аффирмации и построения умозаключения запишите на Кубе третье понятие и продублируйте его.
8. Использование Колец Умозаключений
В набор «Символ Логики» входит пять Колец Умозаключений, несущих на себе кванторные слова для построения логических суждений. Расположение кванторных слов на каждом Кольце рассчитано так, чтобы с их помощью всегда складывались логически правильные умозаключения. Символ логического следования =>, стоящий перед кванторным словом, обозначает результат умозаключения.
Для построения композиции выберите Кольцо Умозаключения и наденьте его на Куб Понятий так, чтобы кванторные слова на Кольце расположились соответствующим образом относительно понятий, записанных на Кубе, образуя вместе с ними требуемые аффирмации.
Надевая Кольцо на Куб Понятий, сначала вставьте один из трех выступов, имеющихся на внутренней части Кольца, в подходящий паз на углу (вершине) Куба. Затем, придерживая Кольцо в этом месте, вставьте остальные выступы Кольца в соответствующие пазы на Кубе. При этом все плоские сегменты Кольца должны расположиться вдоль ребер Куба.
Держите Куб за свободные ребра и вершины, чтобы не стереть надписи.
Для построения композиции выберите Кольцо Умозаключения и наденьте его на Куб Понятий так, чтобы кванторные слова на Кольце расположились соответствующим образом относительно понятий, записанных на Кубе, образуя вместе с ними требуемые аффирмации.
Надевая Кольцо на Куб Понятий, сначала вставьте один из трех выступов, имеющихся на внутренней части Кольца, в подходящий паз на углу (вершине) Куба. Затем, придерживая Кольцо в этом месте, вставьте остальные выступы Кольца в соответствующие пазы на Кубе. При этом все плоские сегменты Кольца должны расположиться вдоль ребер Куба.
Держите Куб за свободные ребра и вершины, чтобы не стереть надписи.
9. Прочтение аффирмаций и суждений
Построенная с помощью элементов набора «Символ Логики» аффирмация или суждение складывается из одного кванторного слова, имеющегося на Кольце Умозаключения, и двух понятий, записанных на смежных гранях Куба Понятий. Для удобного прочтения аффирмации или суждения возьмите Куб с надетым на него Кольцом так, чтобы сегмент Кольца с выбранным кванторным словом расположился над Кубом в горизонтальном положении, чтобы было читаемо кванторное слово.
При этом Куб должен быть обращен к Вам одним из своих ребер, также расположенным горизонтально (как знак тире). Выше и ниже этого ребра, на смежных гранях должны быть видимы (возможно, перевернутыми) записанные на них понятия, входящие в аффирмацию или суждение.
Читайте аффирмацию или суждение, начиная с кванторного слова, следом за ним сверху вниз — два понятия, записанные на двух расположенных столбиком под кванторным словом гранях Куба, разделяя их знаком тире.
Если на какой-то грани имеется знак отрицания «НЕ», он читается перед понятием, записанным на этой грани, образуя контрадикторное понятие.
При этом Куб должен быть обращен к Вам одним из своих ребер, также расположенным горизонтально (как знак тире). Выше и ниже этого ребра, на смежных гранях должны быть видимы (возможно, перевернутыми) записанные на них понятия, входящие в аффирмацию или суждение.
Читайте аффирмацию или суждение, начиная с кванторного слова, следом за ним сверху вниз — два понятия, записанные на двух расположенных столбиком под кванторным словом гранях Куба, разделяя их знаком тире.
Если на какой-то грани имеется знак отрицания «НЕ», он читается перед понятием, записанным на этой грани, образуя контрадикторное понятие.
10. Равнозначные суждения
Каждое суждение, построенное на Кубе Понятий с помощью Кольца Умозаключения, автоматически дополняется равнозначным суждением, которое можно прочесть, повернув Куб на 180 градусов вокруг его вертикальной оси в случае общего суждения или вокруг сагиттальной (передне-задней) оси во всех случаях.
Равнозначное суждение содержит те же понятия и передает ту же мысль, что и исходное суждение, но выраженную иначе, например:
Некоторые мои друзья — веганы = Некоторые веганы — мои друзья
Все не смертельное — полезное = Все не полезное — смертельное.
Все умные — богатые = Только богатые — умные.
Таким образом, любая аффирмация общего вида будет представлена четырьмя логически равносильными высказываниями, например:
1. Все мои помыслы — чистые и благородные;
2. Только чистые и благородные — мои помыслы;
3. Все не чистые и благородные — не мои помыслы;
4. Только не мои помыслы — не чистые и благородные.
Равнозначное суждение содержит те же понятия и передает ту же мысль, что и исходное суждение, но выраженную иначе, например:
Некоторые мои друзья — веганы = Некоторые веганы — мои друзья
Все не смертельное — полезное = Все не полезное — смертельное.
Все умные — богатые = Только богатые — умные.
Таким образом, любая аффирмация общего вида будет представлена четырьмя логически равносильными высказываниями, например:
1. Все мои помыслы — чистые и благородные;
2. Только чистые и благородные — мои помыслы;
3. Все не чистые и благородные — не мои помыслы;
4. Только не мои помыслы — не чистые и благородные.
11. Построение умозаключений
Любое из Колец Умозаключений, в любом положении надетое на Куб Понятий, формирует логически правильное умозаключение, состоящее из трех суждений, содержащих три понятия, записанные на гранях Куба. Два суждения при этом выступают в качестве исходных посылок, а третье в качестве выводимого из них заключения. Заключение помечено символом логического следования =>, стоящим перед его кванторным словом.
Набор «Символ Логики» можно использовать либо для построения умозаключений на основе любых трех произвольно заданных понятий, либо для автоматического получения из двух заданных суждений третьего суждения.
Хотя бы одна из исходных посылок должна быть общего вида. Из двух посылок общего вида всегда выводится заключение. Если одно из двух заданных суждений частное, то оно не всегда может служить исходной посылкой, но в этом случае может служить заключением и использоваться для восстановления пропущенной посылки, как, например, в случае суждений «Все люди — братья» и «Некоторые братья — не родные».
Набор «Символ Логики» можно использовать либо для построения умозаключений на основе любых трех произвольно заданных понятий, либо для автоматического получения из двух заданных суждений третьего суждения.
Хотя бы одна из исходных посылок должна быть общего вида. Из двух посылок общего вида всегда выводится заключение. Если одно из двух заданных суждений частное, то оно не всегда может служить исходной посылкой, но в этом случае может служить заключением и использоваться для восстановления пропущенной посылки, как, например, в случае суждений «Все люди — братья» и «Некоторые братья — не родные».
12. Вывод классических модусов силлогизмов
В классической силлогистике рассматривается девятнадцать основных модусов силлогизмов. Традиционное их изучение построено либо на запоминании, либо на выводе их по неким правилам. С помощью набора «Символ Логики» все их можно легко построить, хотя набор позволяет строить гораздо больше правильных форм умозаключений.
В модусах используются абстрактные понятия, называемые терминами и обозначаемые латинскими буквами S, M, P. Эти символы надо записать на гранях Куба Понятий, продублировав каждый на противоположной грани. Абстрактные суждения при этом имеют в традиционной силлогистике вид, например, «Все S есть M» или «Некоторые M не есть P».
В модусах используются абстрактные понятия, называемые терминами и обозначаемые латинскими буквами S, M, P. Эти символы надо записать на гранях Куба Понятий, продублировав каждый на противоположной грани. Абстрактные суждения при этом имеют в традиционной силлогистике вид, например, «Все S есть M» или «Некоторые M не есть P».
13. Арифметические действия
Набор «Символ Логики» также может быть полезен для объяснения детям арифметических действий. Для этого возьмите Куб с любым Кольцом, надетыми на него, так, чтобы одна из его вершин была обращена к Вам, и были одинаково видны три его грани, при этом одна из граней располагалась сверху и была отделена от двух других видимых граней двумя сегментами Кольца.
На две нижние грани запишите два произвольных слагаемых или два множителя, а на верхней грани запишите соответственно их сумму или произведение. Тогда Кольцо будет обозначать соответственно действие вычитания либо деления. Так, вычитая из числа на верхней грани одно из чисел, расположенных на грани под Кольцом, получаем число на соседней с ним грани.
Например, если на нижних гранях записаны слагаемые 2 и 3, а на верхней их сумма 5, то 5 - 2 = 3 и 5 - 3 = 2. А если на нижних гранях записаны множители 2 и 4, а не верхней их произведение 8, то 8 : 2 = 4 и 8 : 4 = 2.
На две нижние грани запишите два произвольных слагаемых или два множителя, а на верхней грани запишите соответственно их сумму или произведение. Тогда Кольцо будет обозначать соответственно действие вычитания либо деления. Так, вычитая из числа на верхней грани одно из чисел, расположенных на грани под Кольцом, получаем число на соседней с ним грани.
Например, если на нижних гранях записаны слагаемые 2 и 3, а на верхней их сумма 5, то 5 - 2 = 3 и 5 - 3 = 2. А если на нижних гранях записаны множители 2 и 4, а не верхней их произведение 8, то 8 : 2 = 4 и 8 : 4 = 2.
14. Действия с отрицательными числами
Для демонстрации действий с отрицательными числами запишите для каждого числа на противоположной грани Куба соответствующее ему отрицательное число. Если теперь поворачивать Куб с надетым на него Кольцом в разные положения так, чтобы сверху оказывалась одна грань, а две грани под ней были отделены от нее сегментами Кольца, то сумма чисел на нижних гранях всегда будет равна числу на верхней грани, а при вычитании из числа на верхней грани одного из чисел с нижней грани будет получаться второе число с нижней грани. Всего таких положений будет шесть по количеству записанных на гранях Куба чисел.
15. Действия с дробными числами
Аналогичным образом с помощью набора «Символ Логики» демонстрируются действия с дробями. Для этого при описанном выше положении Куба на нижние грани запишите два произвольных множителя, а на верхнюю грань — их произведение. После этого на противоположных гранях Куба запишите дроби с единицей в числителе и исходным числом в знаменателе, то есть, например, для числа 2 на противоположной грани запишите 1/2, а для числа 8 запишите 1/8.
16. Уравнения
Если вместо одного из чисел записать неизвестное х, можно будет строить простые уравнения. Для этого на противоположной грани записать противоположное число -х, если уравнение со сложением (вычитанием), или обратное 1/х, если уравнение с умножением.
Вместо чисел можно записать функции или переменные. Например, на верхней грани записать переменную S, а на нижних гранях переменные V и T, чтобы получить уравнение пути, скорости и времени. Или на верхней грани записать параметр U (напряжение), а на нижних — параметры I (сила тока) и R (сопротивление), чтобы получить закон Ома.
Для тригонометрических функций на верхнюю грань следует записать sin (синус), а на нижние cos (косинус) и tg (тангенс). На грань, противоположную sin, записать обратную ему функцию cosec (косеканс), на грань, противоположную cos,— функцию sec (секанс), на грань, противоположную tg, — функцию ctg (котангенс). Так можно определять, что получается при умножении или делении данных функций друг на друга. Если же расположить Куб так, чтобы три видимые грани не были разделены Кольцом, то при перемножении трех записанных на них функций будет получаться 1, например, sin(x)*ctg(x)*sec(x)=1.
Вместо чисел можно записать функции или переменные. Например, на верхней грани записать переменную S, а на нижних гранях переменные V и T, чтобы получить уравнение пути, скорости и времени. Или на верхней грани записать параметр U (напряжение), а на нижних — параметры I (сила тока) и R (сопротивление), чтобы получить закон Ома.
Для тригонометрических функций на верхнюю грань следует записать sin (синус), а на нижние cos (косинус) и tg (тангенс). На грань, противоположную sin, записать обратную ему функцию cosec (косеканс), на грань, противоположную cos,— функцию sec (секанс), на грань, противоположную tg, — функцию ctg (котангенс). Так можно определять, что получается при умножении или делении данных функций друг на друга. Если же расположить Куб так, чтобы три видимые грани не были разделены Кольцом, то при перемножении трех записанных на них функций будет получаться 1, например, sin(x)*ctg(x)*sec(x)=1.
17. Инсталляция
Из частей набора «Символ Логики» можно создать инсталляцию, символизирующую силу мысли и воображения. Вставьте выступы на внутренней стороне Кольца в три паза на Кубе так, чтобы сегменты Кольца отступали от Куба. Так же присоедините еще одно Кольцо.
Устанавливайте получившуюся фигуру в различные устойчивые положения.
Устанавливайте получившуюся фигуру в различные устойчивые положения.